What is the logical gate speed of a photonic quantum computer?

Terry Rudolph, PsiQuantum & Imperial College London

During a recent visit to the wild western town of Pasadena I got into a shootout at high-noon trying to explain the nuances of this question to a colleague. Here is a more thorough (and less risky) attempt to recover!

tl;dr Photonic quantum computers can perform a useful computation orders of magnitude faster than a superconducting qubit machine. Surprisingly, this would still be true even if every physical timescale of the photonic machine was an order of magnitude longer (i.e. slower) than those of the superconducting one. But they won’t be.

SUMMARY

There is a misconception that the slow rate of entangled photon production from many current (“postselected”) experiments is somehow relevant to the logical speed of a photonic quantum computer. It isn’t, because those experiments don’t use an optical switch.
If we care about how fast we can solve useful problems then photonic quantum computers will eventually win that race. Not only because in principle their components can run faster, but because of fundamental architectural flexibilities which mean they need to do fewer things.
Unlike most quantum systems for which relevant physical timescales are determined by “constants of nature” like interaction strengths, the relevant photonic timescales are determined by “classical speeds” (optical switch speeds, electronic signal latencies etc). Surprisingly, even if these were slower – which there is no reason for them to be – the photonic machine can still compute faster.
In a simple world the speed of a photonic quantum computer would just be the speed at which it’s possible to make small (fixed sized) entangled states. GHz rates for such are plausible and correspond to the much slower MHz code-cycle rates of a superconducting machine. But we want to leverage two unique photonic features: Availability of long delays (e.g. optical fiber) and ease of nonlocal operations, and as such the overall story is much less simple.
If what floats your boat are really slow things, like cold atoms, ions etc., then the hybrid photonic/matter architecture outlined here is the way you can build a quantum computer with a faster logical gate speed than (say) a superconducting qubit machine. You should be all over it.
Magnifying the number of logical qubits in a photonic quantum computer by 100 could be done simply by making optical fiber 100 times less lossy. There are reasons to believe that such fiber is possible (though not easy!). This is just one example of the “photonics is different, photonics is different, ” mantra we should all chant every morning as we stagger out of bed.
The flexibility of photonic architectures means there is much more unexplored territory in quantum algorithms, compiling, error correction/fault tolerance, system architectural design and much more. If you’re a student you’d be mad to work on anything else!

Sorry, I realize that’s kind of an in-your-face list, some of which is obviously just my opinion! Lets see if I can make it yours too

I am not going to reiterate all the standard stuff about how photonics is great because of how manufacturable it is, its high temperature operation, easy networking modularity blah blah blah. That story has been told many times elsewhere. But there are subtleties to understanding the eventual computational speed of a photonic quantum computer which have not been explained carefully before. This post is going to slowly lead you through them.

I will only be talking about useful, large-scale quantum computing – by which I mean machines capable of, at a minimum, implementing billions of logical quantum gates on hundreds of logical qubits.

PHYSICAL TIMESCALES

In a quantum computer built from matter – say superconducting qubits, ions, cold atoms, nuclear/electronic spins and so on, there is always at least one natural and inescapable timescale to point to. This typically manifests as some discrete energy levels in the system, the levels that make the two states of the qubit. Related timescales are determined by the interaction strengths of a qubit with its neighbors, or with external fields used to control it. One of the most important timescales is that of measurement – how fast can we determine the state of the qubit? This generally means interacting with the qubit via a sequence of electromagnetic fields and electronic amplification methods to turn quantum information classical. & Of course, measurements in quantum theory are a pernicious philosophical pit – some people claim they are instantaneous, others that they don’t even happen! Whatever. What we care about is: How long does it take for a readout signal to get to a computer that records the measurement outcome as classical bits, processes them, and potentially changes some future action (control field) interacting with the computer?

For building a quantum computer from optical frequency photons there are no energy levels to point to. The fundamental qubit states correspond to a single photon being either “here” or “there”, but we cannot trap and hold them at fixed locations, so unlike, say, trapped atoms these aren’t discrete energy eigenstates. The frequency of the photons does, in principle, set some kind of timescale (by energy-time uncertainty), but it is far too small to be constraining. The most basic relevant timescales are set by how fast we can produce, control (switch) or detect the photons. While these depend on the bandwidth of the photons used – itself a very flexible design choice – typical components operate in GHz regimes. Another relevant timescale is that we can store photons in a standard optical fiber for tens of microseconds before its probability of getting lost exceeds (say) 10%.

There is a long chain of things that need to be strung together to get from component-level physical timescales to the computational speed of a quantum computer built from them. The first step on the journey is to delve a little more into the world of fault tolerance.

TIMESCALES RELEVANT FOR FAULT TOLERANCE

The timescales of measurement are important because they determine the rate at which entropy can be removed from the system. All practical schemes for fault tolerance rely on performing repeated measurements during the computation to combat noise and imperfection. (Here I will only discuss surface-code fault tolerance, much of what I say though remains true more generally.) In fact, although at a high level one might think a quantum computer is doing some nice unitary logic gates, microscopically the machine is overwhelmingly just a device for performing repeated measurements on small subsets of qubits.

In matter-based quantum computers the overall story is relatively simple. There is a parameter $d$ , the “code distance”, dependent primarily on the quality of your hardware, which is somewhere in the range of 20-40. It takes $d^2$ qubits to make up a logical qubit, so let’s say 1000 of them per logical qubit. (We need to make use of an equivalent number of ancillary qubits as well). Very roughly speaking, we repeat twice the following: each physical qubit gets involved in a small number (say 4-8) of two-qubit gates with neighboring qubits, and then some subset of qubits undergo a single-qubit measurement. Most of these gates can happen simultaneously, so (again, roughly!) the time for this whole process is the time for a handful of two-qubit gates plus a measurement. It is known as a code cycle and the time it takes we denote $T_{cc}$ . For example, in superconducting qubits this timescale is expected to be about 1 microsecond, for ion-trap qubits about 1 millisecond. Although variations exist, lets stick to considering a basic architecture which requires repeating this whole process on the order of $d$ & times in order to complete one logical operation (i.e., a logical gate). So, the time for a logical gate would be $d\times T_{cc}$ , this sets the effective logical gate speed.

If you zoom out, each code cycle for a single logical qubit is therefore built up in a modular fashion from $d^2$ & copies of the same simple quantum process – a process that involves a handful of physical qubits and gates over a handful of time steps, and which outputs a classical bit of information – a measurement outcome. I have ignored the issue of what happens to those measurement outcomes. Some of them will be sent to a classical computer and processed (decoded) then fed back to control systems and so on. That sets another relevant timescale (the reaction time) which can be of concern in some approaches, but early generations of photonic machines – for reasons outlined later – will use long delay lines, and it is not going to be constraining.

In a photonic quantum computer we also build up a single logical qubit code cycle from $d^2$ & copies of some quantum stuff. In this case it is from $d^2$ & copies of an entangled state of photons that we call a resource state. The number of entangled photons comprising one resource state depends a lot on how nice and clean they are, lets fix it and say we need a 20-photon entangled state. (The noisier the method for preparing resource states the larger they will need to be). & No sequence of gates is performed on these photons. Rather, photons from adjacent resource states get interfered at a beamsplitter and immediately detected – a process we call fusion. You can see a toy version in this animation:

Highly schematic depiction of photonic fusion based quantum computing. An array of 25 resource state generators each repeatedly create resource states of 6 entangled photons, depicted as a hexagonal ring. Some of the photons in each ring are immediately fused (the yellow flashes) with photons from adjacent resource states, the fusion measurement outputs classical bits of information. One photon from each ring gets delayed for one clock cycle and fused with a photon from the next clock cycle.

Measurements destroy photons, so to ensure continuity from one time step to the next some photons in a resource state get delayed by one time step to fuse with a photon from the subsequent resource state – you can see the delayed photons depicted as lit up single blobs if you look carefully in the animation.

The upshot is that the zoomed out view of the photonic quantum computer is very similar to that of the matter-based one, we have just replaced the handful of physical qubits/gates of the latter with a 20-photon entangled state. (And in case it wasn’t obvious – building a bigger computer to do a larger computation means generating more of the resource states, it doesn’t mean using larger and larger resource states.)

If that was the end of the story it would be easy to compare the logical gate speeds for matter-based and photonic approaches. We would only need to answer the question “how fast can you spit out and measure resource states?”. Whatever the time for resource state generation, $T_{RSG}$ , the time for a logical gate would be $d\times T_{RSG}$ & and the photonic equivalent of $T_{cc}$ & would simply be $T_{RSG}$ . (Measurements on photons are fast and so the fusion time becomes effectively negligible compared to $T_{RSG}$ .) An easy argument could then be made that resource state generation at GHz rates is possible, therefore photonic machines are going to be orders of magnitude faster, and this article would be done! And while I personally do think its obvious that one day this is where the story will end, in the present day and age….

… there are two distinct ways in which this picture is far too simple.

FUNKY FEATURES OF PHOTONICS, PART I

& The first over-simplification is based on facing up to the fact that building the hardware to generate a photonic resource state is difficult and expensive. We cannot afford to construct one resource state generator per resource state required at each time step. However, in photonics we are very fortunate that it is possible to store/delay photons in long lengths of optical fiber with very low error rates. This lets us use many resource states all produced by a single resource state generator in such a way that they can all be involved in the same code-cycle. So, for example, all $d^2$ & resource states required for a single code cycle may come from a single resource state generator:

Here the 25 resource state generators of the previous figure are replaced by a single generator that “plays fusion games with itself” by sending some of its output photons into either a delay of length 5 or one of length 25 times the basic clock cycle. We achieve a massive amplification of photonic entanglement simply by increasing the length of optical fiber used. By mildly increasing the complexity of the switching network a photon goes through when it exits the delay, we can also utilize small amounts of (logarithmic) nonlocal connectivity in the network of fusions performed (not depicted), which is critical to doing active volume compiling (discussed later). &

You can see an animation of how this works in the figure – a single resource state generator spits out resource states (depicted again as a 6-qubit hexagonal ring), and you can see a kind of spacetime 3d-printing of entanglement being performed. We call this game interleaving. In the toy example of the figure we see some of the qubits get measured (fused) immediately, some go into a delay of length $5\times T_{RSG}$ & and some go into a delay of length $25\times T_{RSG}$ . &

So now we have brought another timescale into the photonics picture, the length of time $T_{DELAY}$ & that some photons spend in the longest interleaving delay line. We would like to make this as long as possible, but the maximum time is limited by the loss in the delay (typically optical fiber) and the maximum loss our error correcting code can tolerate. A number to have in mind for this (in early machines) is a handful of microseconds – corresponding to a few Km of fiber.

The upshot is that ultimately the temporal quantity that matters most to us in photonic quantum computing is:

What is the total number of resource states produced per second?

It’s important to appreciate we care only about the total rate of resource state production across the whole machine – so, if we take the total number of resource state generators we have built, and divide by $T_{RSG}$ , we get this total rate of resource state generation that we denote $\Gamma_{RSG}$ . & Note that this rate is distinct from any physical clock rate, as, e.g., 100 resource state generators running at 100MHz, or 10 resource state generators running at 1GHz, or 1 resource state generator running at 10GHz all yield the same total rate of resource state production $\Gamma_{RSG}=10\mathrm{GHz.}$

The second most important temporal quantity is $T_{DELAY}$ , the time of the longest low-loss delay we can use.

We then have that the total number of logical qubits in the machine is:

$N_{LOGICAL}=\frac{T_{DELAY}\times\Gamma_{RSG}}{d^2}$

You can see this is proportional to $T_{DELAY}\times\Gamma_{RSG}$ & which is effectively the total number of resource states “alive” in the machine at any given instant of time, including all the ones stacked up in long delay lines. This is how we leverage optical fiber delays for a massive amplification of the entanglement our hardware has available to compute with.

The time it takes to perform a logical gate is determined both by $\Gamma_{RSG}$ & and by the total number of resource states that we need to consume for every logical qubit to undergo a gate. Even logical qubits that appear to not be part of a gate in that time step do, in fact, undergo a gate – the identity gate – because they need to be kept error free while they “idle”. & As such the total number of resource states consumed in a logical time step is just $d^3\times N_{LOGICAL}$ & and the logical gate time of the machine is

$T_{LOGICAL}=\frac{d^3\times N_{LOGICAL}}{\Gamma_{RSG}} =d\times T_{DELAY}$ .

Because $T_{DELAY}$ & is expected to be about the same as $T_{cc}$ & for superconducting qubits (microseconds), the logical gate speeds are comparable.

At least they are, until…………

FUNKY FEATURES OF PHOTONICS, PART II

But wait! There’s more.

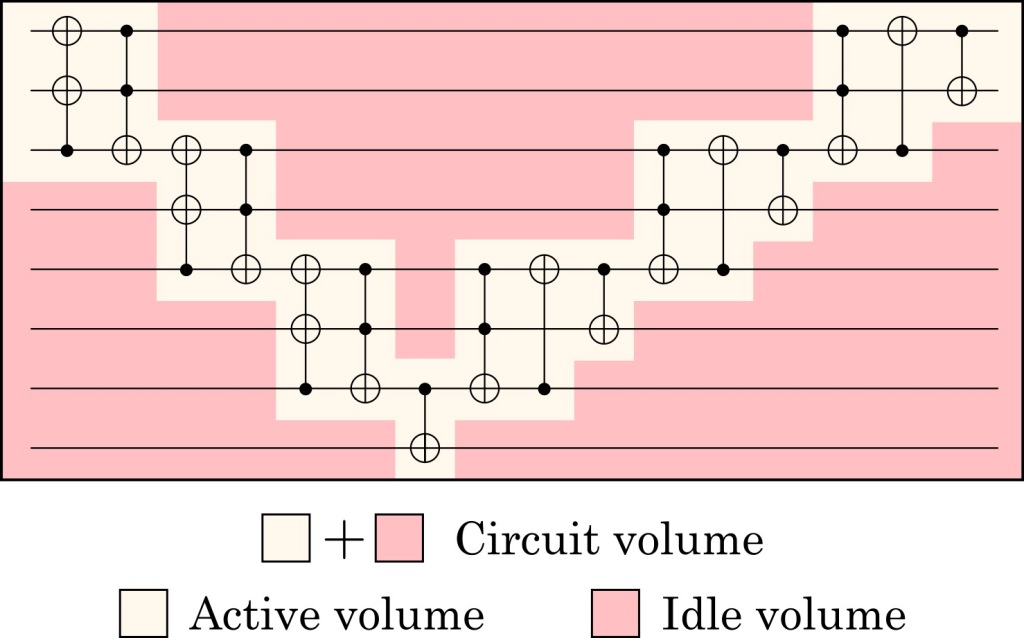
The second way in which unique features of photonics play havoc with the simple comparison to matter-based systems is in the exciting possibility of what we call an active-volume architecture.

A few moments ago I said:

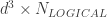
Even logical qubits that seem to not be part of a gate in that time step undergo a gate – the identity gate – because they need to be kept error free while they “idle”.& As such the total number of resource states consumed is just $d^3\times N_{LOGICAL}$

and that was true. Until recently.

It turns out that there is a way of eliminating the majority of consumption of resources expended on idling qubits! This is done by some clever tricks that make use of the possibility of performing a limited number of non-nearest neighbor fusions between photons. It’s possible because photons are not anyway stuck in one place, and they can be passed around readily without interacting with other photons. (Their quantum crosstalk is exactly zero, they do really seem to despise each other.)

What previously was a large volume of resource states being consumed for “thumb-twiddling”, can instead all be put to good use doing non-trivial computational gates. & Here is a simple quantum circuit with what we mean by the active volume highlighted:

Now, for any given computation the amount of active volume will depend very much on what you are computing. & There are always many different circuits decomposing a given computation, some will use more active volume than others. This makes it impossible to talk about “what is the logical gate speed” completely independent of considerations about the computation actually being performed.

In this recent paper https://arxiv.org/abs/2306.08585 Daniel Litinski considers breaking elliptic curve cryptosystems on a quantum computer. In particular, he considers what it would take to run the relevant version of Shor’s algorithm on a superconducting qubit architecture with a $T_{cc}=1$ microsecond code cycle – the answer is roughly that with 10 million physical superconducting qubits it would take about 4 hours (with an equivalent ion trap computer the time balloons to more than 5 months).

He then compares solving the same problem on a machine with an active volume architecture. Here is a subset of his results:

Recall that $T_{DELAY}$ & is the photonics parameter which is roughly equivalent to the code cycle time. Thus taking $T_{DELAY}=$ 1 microsecond compares to the expected $T_{cc}$ for superconducting qubits. Imagine we can produce resource states at & $\Gamma_{RSG}=3.5\mathrm{THz}$ . This could be 6000 resource state generators each producing resource states at $1/T_{RSG}=580\mathrm{MHz}$ or 3500 generators producing them at 1GHz for example. Then the same computation would take 58 seconds, instead of four hours, a speedup by a factor of more than 200!

Now, this whole blog post is basically about addressing confusions out there regarding physical versus computational timescales. So, for the sake of illustration, let me push a purely theoretical envelope: What if we can’t do everything as fast as in the example just stated? What if our rate of total resource state generation was 10 times slower, i.e. & $\Gamma_{RSG}=350\mathrm{GHz}$ ? And what if our longest delay is ten times longer, i.e. $T_{DELAY}=10$ microseconds (so as to be much slower than $T_{cc}$ )?& Furthermore, for the sake of illustration, lets consider a ridiculously slow machine that achieves $\Gamma_{RSG}=350 \mathrm{GHz}$ by building 350 billion resource state generators that can each produce resource states at only 1Hz. Yes, you read that right.

The fastest device in this ridiculous machine would only need to be a (very large!) slow optical switch operating at 100KHz (due to the chosen $T_{DELAY}$ ).& And yet this ridiculous machine could still solve the problem that takes a superconducting qubit machine four hours, in less than 10 minutes.

To reiterate:

Despite all the “physical stuff going on” in this (hypothetical, active-volume) photonic machine running much slower than all the “physical stuff going on” in the (hypothetical, non-active-volume) superconducting qubit machine, we see the photonic machine can still do the desired computation 25 times faster!

Hopefully the fundamental murkiness of the titular question “what is the logical gate speed of a photonic quantum computer” is now clear! Put simply: Even if it did “fundamentally run slower” (it won’t), it would still be faster. Because it has less stuff to do. It’s worth noting that the 25x increase in speed is clearly not based on physical timescales, but rather on the efficient parallelization achieved through long-range connections in the photonic active-volume device. If we were to scale up the hypothetical 10-million-superconducting-qubit device by a factor of 25, it could potentially also complete computations 25 times faster. However, this would require a staggering 250 million physical qubits or more. Ultimately, the absolute speed limit of quantum computations is set by the reaction time, which refers to the time it takes to perform a layer of single-qubit measurements and some classical processing. Early-generation machines will not be limited by this reaction time, although eventually it will dictate the maximum speed of a quantum computation. But even in this distant-future scenario, the photonic approach remains advantageous. As classical computation and communication speed up beyond the microsecond range, slower physical measurements of matter-based qubits will hinder the reaction time, while fast single-photon detectors won’t face the same bottleneck.

In the standard photonic architecture we saw that $T_{LOGICAL}$ & would scale proportionally with& $T_{DELAY}$ & – that is, adding long delays would slow the logical gate speed (while giving us more logical qubits). But remarkably the active-volume architecture allows us to exploit the extra logical qubits without incurring a big negative tradeoff. I still find this unintuitive and miraculous, it just seems to so massively violate Conservation of Trouble.

With all this in mind it is also worth noting as an aside that optical fibers made from (expensive!) exotic glasses or with funky core structures are theoretically calculated to be possible with up to 100 times less loss than conventional fiber – therefore allowing for an equivalent scaling of $T_{DELAY}$ . How many approaches to quantum computing can claim that perhaps one day, by simply swapping out some strands of glass, they could instantaneously multiply the number of logical qubits in the machine from (say) 100 to 10000? Even a (more realistic) factor of 10 would be incredible.

Obviously for pedagogical reasons the above discussion is based around the simplest approaches to logic in both standard and active-volume architectures, but more detailed analysis shows that conclusions regarding total computational time speedup persist even after known optimizations for both approaches.

Now the reason I called the example above a “ridiculous machine” is that even I am not cruel enough to ask our engineers to assemble 350 billion resource state generators. Fewer resource state generators running faster is desirable from the perspective of both sweat and dollars.

We have arrived then at a simple conclusion: what we really need to know is “how fast and at what scale can we generate resource states, with as large a machine as we can afford to build”.

HOW FAST COULD/SHOULD WE AIM TO DO RESOURCE STATE GENERATION?

In the world of classical photonics – such as that used for telecoms, LIDAR and so on – very high speeds are often thrown around: pulsed lasers and optical switches readily run at 100’s of GHz for example. On the quantum side, if we produce single photons via a probabilistic parametric process then similarly high repetition rates have been achieved. (This is because in such a process there are no timescale constraints set by atomic energy levels etc.) Off-the-shelf single photon avalanche photodiode detectors can count photons at multiple GHz.

Seems like we should be aiming to generate resource states at 10’s of GHz right?

Well, yes, one day – one of the main reasons I believe the long-term future of quantum computing is ultimately photonic is because of the obvious attainability of such timescales. [Two others: it’s the only sensible route to a large-scale room temperature machine; eventually there is only so much you can fit in a single cryostat, so ultimately any approach will converge to being a network of photonically linked machines].

In the real world of quantum engineering there are a couple of reasons to slow things down: (i) It relaxes hardware tolerances, since it makes it easier to get things like path lengths aligned, synchronization working, electronics operating in easy regimes etc & (ii) in a similar way to how we use interleaving during a computation to drastically reduce the number of resource state generators we need to build, we can also use (shorter than $T_{DELAY}$ length) delays to reduce the amount of hardware required to assemble the resource states in the first place and (iii) We want to use multiplexing.

Multiplexing is often misunderstood. The way we produce the requisite photonic entanglement is probabilistic. Producing the whole 20-photon resource state in a single step, while possible, would have very low probability. The way to obviate this is to cascade a couple of higher probability, intermediate, steps – selecting out successes (more on this in the appendix). While it has been known since the seminal work of Knill, Laflamme and Milburn two decades ago that this is a sensible thing to do, the obstacle has always been the need for a high performance (fast, low loss) optical switch. Multiplexing introduces a new physical “timescale of convenience” – basically dictated by latencies of electronic processing and signal transmission.

The brief summary therefore is: Yeah, everything internal to making resource states can be done at GHz rates, but multiple design flexibilities mean the rate of resource state generation is itself a parameter that should be tuned/optimized in the context of the whole machine, it is not constrained by fundamental quantum things like interaction energies, rather it is constrained by the speeds of a bunch of purely classical stuff.

I do not want to leave the impression that generation of entangled photons can only be done via the multistage probabilistic method just outlined. Using quantum dots, for example, people can already demonstrate generation of small photonic entangled states at GHz rates (see e.g. https://www.nature.com/articles/s41566-022-01152-2). Eventually, direct generation of photonic entanglement from matter-based systems will be how photonic quantum computers are built, and I should emphasize that its perfectly possible to use small resource states (say, 4 entangled photons) instead of the 20 proposed above, as long as they are extremely clean and pure.& In fact, as the discussion above has hopefully made clear: for quantum computing approaches based on fundamentally slow things like atoms and ions, transduction of matter-based entanglement into photonic entanglement allows – by simply scaling to more systems – evasion of the extremely slow logical gate speeds they will face if they do not do so.

Right now, however, approaches based on converting the entanglement of matter qubits into photonic entanglement are not nearly clean enough, nor manufacturable at large enough scales, to be compatible with utility-scale quantum computing. And our present method of state generation by multiplexing has the added benefit of decorrelating many error mechanisms that might otherwise be correlated if many photons originate from the same device.

So where does all this leave us?

I want to build a useful machine. Lets back-of-the-envelope what that means photonically. Consider we target a machine comprising (say) at least 100 logical qubits capable of billions of logical gates. (From thinking about active volume architectures I learn that what I really want is to produce as many “logical blocks” as possible, which can then be divvied up into computational/memory/processing units in funky ways, so here I’m really just spitballing an estimate to give you an idea).

Staring at &

$N_{LOGICAL}=\frac{T_{DELAY}\times\Gamma_{RSG}}{d^2}$

and presuming $d^2\approx1000$ and $T_{DELAY}$ & is going to be about 10 microseconds, we need to be producing resource states at a total rate of at least $\Gamma_{RSG}=10\mathrm{GHz}$ . & As I hope is clear by now, as a pure theoretician, I don’t give a damn if that means 10000 resource state generators running at 1MHz, 100 resource state generators running at 100MHz, or 10 resource state generators running at 1GHz. However, the fact this flexibility exists is very useful to my engineering colleagues – who, of course, aim to build the smallest and fastest possible machine they can, thereby shortening the time until we let them head off for a nice long vacation sipping mezcal margaritas on a warm tropical beach.

None of these numbers should seem fundamentally indigestible, though I do not want to understate the challenge: all never-before-done large-scale engineering is extremely hard.

But regardless of the regime we operate in, logical gate speeds are not going to be the issue upon which photonics will be found wanting.

REAL-WORLD QUANTUM COMPUTING DESIGN

Now, I know this blog is read by lots of quantum physics students. If you want to impact the world, working in quantum computing really is a great way to do it. The foundation of everything round you in the modern world was laid in the 40’s and 50’s when early mathematicians, computer scientists, physicists and engineers figured out how we can compute classically. Today you have a unique opportunity to be part of laying the foundation of humanity’s quantum computing future. Of course, I want the best of you to work on a photonic approach specifically (I’m also very happy to suggest places for the worst of you to go work). Please appreciate, therefore, that these final few paragraphs are my very biased – though fortunately totally correct – personal perspective!

The broad features of the photonic machine described above – it’s a network of stuff to make resource states, stuff to fuse them, and some interleaving modules, has been fixed now for several years (see the references).

Once we go down even just one level of detail, a myriad of very-much-not-independent questions arise: What is the best resource state? What series of procedures is optimal for creating that state? What is the best underlying topological code to target? What fusion network can build that code? What other things (like active volume) can exploit the ability for photons to be easily nonlocally connected? What types of encoding of quantum information into photonic states is best? What interferometers generate the most robust small entangled states? What procedures for systematically growing resource states from smaller entangled states are most robust or use the least amount of hardware? How can we best use measurements and classical feedforward/control to mitigate error accumulation?

Those sorts of questions cannot be meaningfully addressed without going down to another level of detail, one in which we do considerable modelling of the imperfect devices from which everything will be built – modelling that starts by detailed parameterization of about 40 component specifications (ranging over things like roughness of silicon photonic waveguide walls, stability of integrated voltage drivers, precision of optical fiber cutting robots,….. Well, the list goes on and on). We then model errors of subsystems built from those components, verify against data, and proceed.

The upshot is none of these questions have unique answers! There just isn’t “one obviously best code” etc. In fact the answers can change significantly with even small variations in performance of the hardware. This opens a very rich design space, where we can establish tradeoffs and choose solutions that optimize a wide variety of practical hardware metrics.

In photonics there is also considerably more flexibility and opportunity than with most approaches on the “quantum side” of things. That is, the quantum aspects of the sources, the quantum states we use for encoding even single qubits, the quantum states we should target for the most robust entanglement, the topological quantum logical states we target and so on, are all “on the table” so to speak.

Exploring the parameter space of possible machines to assemble, while staying fully connected to component level hardware performance, involves both having a very detailed simulation stack, and having smart people to help find new and better schemes to test in the simulations. It seems to me there are far more interesting avenues for impactful research than more established approaches can claim. Right now, on this planet, there are only around 30 people engaged seriously in that enterprise. It’s fun. Perhaps you should join in?

REFERENCES

A surface code quantum computer in silicon https://www.science.org/doi/10.1126/sciadv.1500707. Figure 4 is a clear depiction of the circuits for performing a code cycle appropriate to a generic 2d matter-based architecture.

Fusion-based quantum computation https://arxiv.org/abs/2101.09310

Interleaving: Modular architectures for fault-tolerant photonic quantum computing https://arxiv.org/abs/2103.08612

Active volume: An architecture for efficient fault-tolerant quantum computers with limited non-local connections https://arxiv.org/abs/2211.15465

How to compute a 256-bit elliptic curve private key with only 50 million Toffoli gates https://arxiv.org/abs/2211.15465

Conservation of Trouble: https://arxiv.org/abs/quant-ph/9902010

APPENDIX – A COMMON MISCONCEPTION

Here is a common misconception: Current methods of producing ~20 photon entangled states succeed only a few times per second, so generating resource states for fusion-based quantum computing is many& orders of magnitude away from where it needs to be.

This misconception arises from considering experiments which produce photonic entangled states via single-shot spontaneous processes and extrapolating them incorrectly as having relevance to how resource states for photonic quantum computing are assembled.

Such single-shot experiments are hit by a “double whammy”. The first whammy is that the experiments produce some very large and messy state that only has a tiny amplitude in the component of the desired entangled state. Thus, on each shot, even in ideal circumstances, the probability of getting the desired state is very, very small. Because billions of attempts can be made each second (as mentioned, running these devices at GHz speeds is easy) it does occasionally occur. But only a small number of times per second.

The second whammy is that if you are trying to produce a 20-photon state, but each photon gets lost with probability 20%, then the probability of you detecting all the photons – even if you live in a branch of the multiverse where they have been produced – is reduced by a factor of $0.8^{20}$ . Loss reduces the rate of production considerably.

Now, photonic fusion-based quantum computing could not be based on this type of entangled photon generation a